
| Moebius, ein
Modellbildungssystem für Mathematik und Naturwissenschaften |
|
|
Simulation zur Corona-Pandemie herunterladen. Simulation zur Corona-Pandemie mit Moebius Natürlich kann Moebius keine komplexe Simulation einer Pandemie mit realen Daten und daraus folgenden Vorhersagen leisten. Es genügen aber schon wenige Zeilen um das Abflachen der Kurve der Infizierten durch eine Kontaktreduzierung zu zeigen und auch zu verstehen. Programm zur Simulation der Ausbreitung einer Infektion: | |
| NeuInfektionen = InfFaktor*(alle-Immune-Kranke)*Kranke | Die erste Zeile ist die entscheidende Zeile. Die Neuinfektionen sind proportional zu den noch nicht Infizierten (also die gesamte Bevölkerung minus die schon Immunen und die Kranken). Außerdem sind sie proportional zu den Kranken, die andere anstecken können. Um zu verstehen, dass sie dann zum Produkt dieser beiden Faktoren proportional sind, kann folgendes Beispiel helfen. Wenn in jeder Tüte Brötchen gleich viele Brötchen sind, dann ist die Gesamtzahl der Brötchen proportional zur Anzahl der Tüten. Sie ist aber auch proportional zur Anzahl der Brötchen in jeder Tüte. Man erhält die Gesamtzahl als Produkt der beiden Zahlen. Für die Anzahl der Neuinfektionen spielt der Proportionalitätsfaktor InfFaktor eine entscheidende Rolle. Je mehr Kontakte zwischen Kranken und anderen Personen stattfinden, desto größer ist er. |
| if NeuInfektionen < 0 then NeuInfektionen = 0 | Weil wir in großen Schritten rechnen, kann die Anzahl der Neuinfektionen negativ werden. Das wird durch diese Zeile verhindert. |
|
Kranke = Kranke + NeuInfektionen Immune = Immune + kFaktor*Kranke Kranke = Kranke - kFaktor*Kranke |
Diese drei Zeilen erklären sich fast von selbst. Entscheidend ist, dass bei jedem Zeitschritt eine gewisse Anzahl der Kranken wieder gesund wird. Dies steuert der Faktor kFaktor. |
| t = t + 1 | Zuletzt brauchen wir noch eine Zeitachse. |
Ergebnis: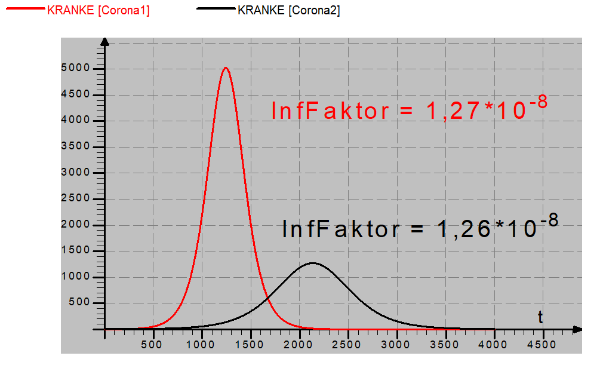
|
|
| Schon eine geringfügige Verkleinerung des Infektionsfaktors führt zu einer wesentlich kleineren Maximalzahl von Kranken. Allerdings wird dafür der Zeitraum der Pandemie größer. | |
| Hier noch die Startwerte für die Simulation: |
INFFAKTOR: 1,27E-8 bzw. 1,26E-8 ALLE: 80000000 IMMUNE: 0 KRANKE: 1 KFAKTOR: 0,5 T: 0 |
|
Kann man auch mit realen Zahlen rechnen?
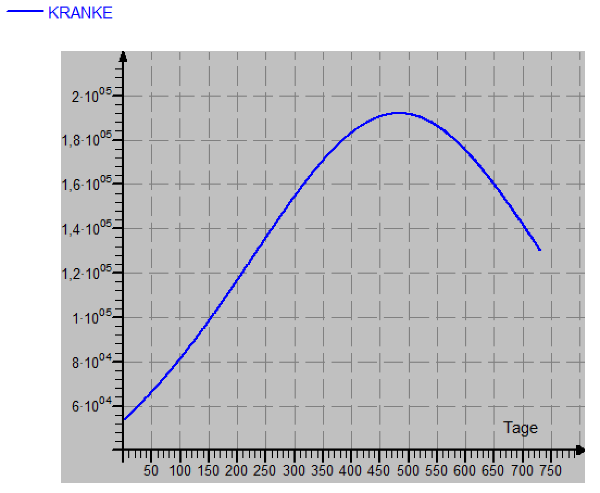
Am 28.März 2020 waren ca. 54000 Menschen positiv auf Corona getestet. Es kamen ca 4400 Neuinfektionen an einem Tag hinzu. Angesichts von 80 Mio. Menschen kann man in der Rechnung die Immunen zu diesem Zeitpunkt vernachlässigen. Dann kann man den Infektionsfaktor aus der ersten Zeile des Moebius-Programms berechnen: InfFaktor = 4400/(8E7 * 54000) = 1E-9. Geht man von einer Krankheitsdauer von 14 Tagen aus, dann gesundet jeden Tag ungefähr 1/14 der Kranken. Es ergeben sich also die Startwerte: | |
|
Update am 20.4.2020: Wie könnte es weitergehen? Am Montag 20.4.2020 treten erste Erleichterungen der Kontaktverbote in Kraft. Deshalb bietet es sich an, einmal den Verlauf mit den aktuellen Zahlen zu prognostizieren. Am 17.4.2020 gab es 3133 Neuinfektionen, 83114 Menschen waren in Deutschland von einer Infektion genesen, 56588 akut krank. Berechnet man mit diesen Zahlen den Infektionsfaktor, so erhält man ungefähr 0,7E-10. Trägt man die neuen Werte mit T=20 (vergangene Tage seit dem 27.3.) in Moebius ein, erhält man die rote Kurve. Das heißt, das Virus könnte mit den Maßnahmen von Anfang April theoretisch (!) eingedämmt werden. Wir können nun mit Spannung verfolgen, wie sich die Lockerung auswirken wird... 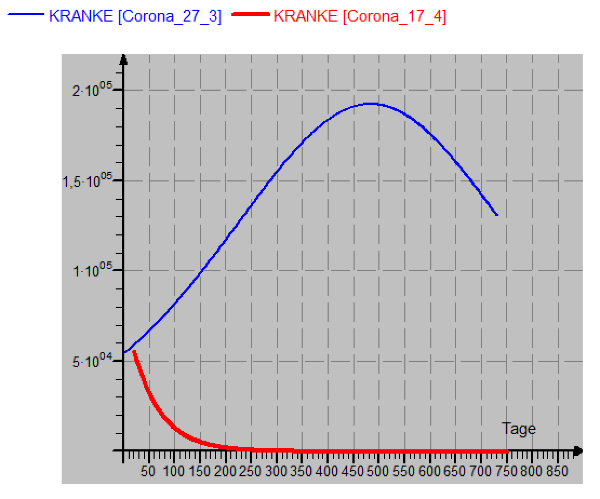
|
|
|
Update am 7.6.2020: Und wie ist es weiter gegangen? Vergleicht man den realen Verlauf der an Covid-19 Erkrankten mit den von dem extrem einfachen Modell am 17.4.2020 prognostizierten Zahlen, dann staunt man nicht schlecht, wie gut die Realität mit der Prognose übereinstimmt. Zwar beträgt die durchschnittliche Abweichung 20%, aber der prinzipielle Verlauf ist nahezu identisch. Konnte man das von einem so einfachen Modell erwarten? Noch ein Hinweis zur Bedienung: Ich habe die Daten aus einer Moebius-Tabelle über die Zwischenablage in eine Tabellenkalkulation eingefügt und zusammen mit den realen Daten dann in der Tabellenkalkulation in ein Schaubild übertragen. 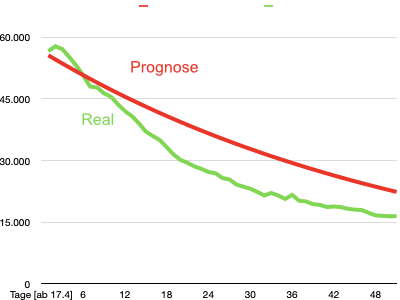
|
|
|
Update am 17.1.2021: Wie gefährlich ist die ansteckendere Mutation des Virus? Heute treffen sich die Ministerpräsidenten, um über weitere Beschränkungen zu beraten, weil eine 70% ansteckendere Mutation des Virus droht. Man kann die Ursache für diese Beratungen unmittelbar mit den realen Daten der Woche vom 11.1. bis 17.1. aufzeigen. Leider sind diese Daten nicht sehr zuverlässig. Trotzdem kann man deutlich sehen, dass ein ansteckenderes Virus den Pandemie-Verlauf erheblich beeinfussen kann. In der besgaten Woche gab es täglich durchschnittlich ca. 15600 Neuinfektionen. Es waren durchschnittlich 320000 Menschen akut krank und damit eine mögliche Infektionsquelle. Wir berechnen wie in obigem Beispiel den Infektionsfaktor auf 6,1E-10. Würde das Virus 70% ansteckender sein, dann gäbe es 1,7 fache Neuinfektionen und damit einen Infektionsfaktor 1E-9. Mit diesen Werten kann man sehen, dass der Lockdown nicht ausreicht, um die neue Variante zu besiegen. 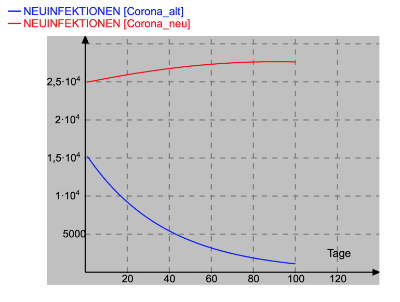 Eine 7-Tage-Inzidenz von 50 auf 100000 würde man mit den derzeitigen Maßnahmen nach 38 Tagen beim herkömmlichen Virus erreichen. Mit der Mutation läge diese nach 38 Tagen bei 233. Update am 28.7.2021: Wie kann eine Mutation eine andere Mutation des Virus verdrängen? Ich habe nun längere Zeit keine Updates mehr gemacht, weil die Situation durch Impfung und Testen so komplex geworden ist, dass eine Simulation zu viele Parameter hat. Trotzdem möchte ich hier eine mathematische Überlegung einbringen. Ich habe mich in den letzten Tagen mit folgendem Problem beschäftigt: In den Medien wird immer berichtet, dass die Delta-Variante die anderen Varianten verdrängt. Ich habe das nicht verstanden, weil doch immer noch genügend Menschen da sind, die sich mit der beta-Variante anstecken können. Nun habe ich die Lösung. Wenn z.B. die alpha-Variante einen R-Wert von 0,8 hat, dann ist bei den vorherrschenden Maßnahmen der Verlauf exponentiell fallend. Kommt nun eine beta-Variante, die ansteckender ist, hinzu, dann ist deren R-Wert über 1. D.h. die eine Variante nimmt exponentiell ab und die andere exponentiell zu. Es ist also eine falsche Argumentation, wenn man von Verdrängen spricht. Vielmehr könnte es z.B. jetzt, da Delta zunimmt, ein noch ansteckenderes Epsilon gleichzeitig mit Delta wachsen. Es kommt eben darauf an, ob die Maßnahmen den R-Wert entsprechend senken. Wenn man das auf Großbritannien überträgt, dann können dort bald viele Varianten nebeneinander existieren, wenn alles aufgemacht wird. |
|
Klicken Sie auf das Logo, um in den Apple App Store zu wechseln.

Hier erfahren Sie mehr über Schullizenzen bei Apple.
Klicken Sie auf das Logo, um in den Microsoft App Store zu wechseln.

Wenn Sie früher eine Schullizenz für Moebius erworben haben, dann können Sie hier einen Download-Link zu der älteren Version anfordern.
Download-Link anfordern
Schülerinnen und Schüler können hier eine kostenlose Version für zu Hause herunterladen. Diese darf nicht im Unterricht eingesetzt werden!
Der Freistaat Sachsen hat eine Landeslizenz für das Programm Moebius erworben: Diese erlaubt die Installation der Moebius-Software auf allen Computern der allgemeinbildenden Gymnasien, Abendgymnasien, Kollegs, der beruflichen Gymnasien und Fachoberschulen des Freistaats Sachsen, des Sächsischen Bildungsinstituts, der Sächsischen Bildungsagentur und des Sächsischen Staatsministeriums für Kultus. Schulen aus anderen Bundesländern sind nicht berechtigt diese Programmversion zu verwenden. Klicken Sie hier, wenn Sie berechtigt sind, diese Version herunterzuladen.